Compound Interest Formula with Examples

What is Compound Interest?

Compound interest is the interest that you earn on the principal and interest together over a period of time. When you add the earned interest into your principal amount, makes you earn more interest, which leads to compounding your returns. That means, upon reinvesting your earnings, you will earn interest. In this, earned interest is reinvested into the principal and earn compounding interest.

The interest accumulated at regular intervals is added with the principal amount and the interest is then calculated for the next time period.

Compound interest absolutely means “interest on the interest”. When it comes to simple interest, earned interest is not compounded and it is calculated only on the principal amount.

Let’s take a look at the difference on simple interest and compound interest.

Time Period	Simple Interest @10%	Compound Interest @10%
Invest	10,000	10,000
1 year	11,000	11,000
2 years	12,000	12,100
5 years	15,000	16,105
10 years	20,000	25,937
20 years	30,000	67,275
30 years	40,000	174,494

---

Let’s take a look at the difference on simple interest and compound interest.

Year	Yearly Interest	Total Interest	Balance
1	$1000	$1000	$11000
2	$1100	$2100	$12100
3	$1210	$3310	$13310
4	$1331	$4641	$14641
5	$1464.1	$6105.1	$16105.1
6	$1610.51	$7715.61	$17715.61
7	$1771.56	$9487.17	$19487.17
8	$1948.72	$11435.89	$21435.89
9	$2143.59	$13579.48	$23579.48
10	$2357.94	$15937.42	$25937.42
11	$2593.75	$18531.17	$28531.17
12	$2853.11	$21384.28	$31384.28
13	$3138.43	$24522.71	$34522.71
14	$3452.27	$27974.99	$37974.98
15	$3797.5	$31772.49	$41772.48
16	$4177.25	$35949.74	$45949.73
17	$4594.97	$40544.71	$50544.7
18	$5054.47	$45599.18	$55599.17
19	$5559.92	$51159.1	$61159.09
20	$6115.91	$57275.01	$67275
21	$6727.5	$64002.51	$74002.5
22	$7400.25	$71402.76	$81402.75
23	$8140.27	$79543.04	$89543.02
24	$8954.31	$88497.34	$98497.33
25	$9849.73	$98347.07	$108347.06
26	$10834.71	$109181.78	$119181.77
27	$11918.17	$121099.95	$131099.94
28	$13110	$134209.95	$144209.94
29	$14420.99	$148630.94	$158630.93
30	$15863.09	$164494.03	$174494.02

Compound interest

The compound interest formula calculator is a very relevant idea that allows you to realize where and how you handle your money and can also allow you to get a greater return on investment and savings. We can’t say but any time the calculator used for compound interest may work against you, particularly if you pay the interest on your loan.

If interest is attached to the total gain of an asset, it, therefore, represents a compound interest, such that the general interest is attached to the capital number.

The below is an explanation that allows you to better grasp the compound interest using a compound interest calculator.

Assume you make a 4-year investment of $ 40000 in a fixed deposit and a 10-percent interest rate so you get about $ 4000 during the first year.

Manually it wouldn't get the same outcome, but you can get the 100 percent per reality with both the help of such a compound interest calculator. It also requires a long time to do manually and measures the compound interest in seconds with the aid of such a calculator.

You can figure out just how often the compound interest will indeed be gained on your savings using this compound interest calculator. You can measure the compound interest monthly, half-yearly, quarterly with this compound interest calculator, or though you prefer to calculate compound interest on one particular day. It plays a major role for an interest compound calculator that is interpreted and used by you as helpful and helpful by way of a compound interest calculator.

Overview of Compound interest formula

In today’s generation, we use a calculator for any sort of calculation because we had made ourselves very oriented on the outcome which should be more than 100 percent accurate, but manually it may not be as feasible or accurate as of the calculator. In making big predictions in seconds, calculators play a major role. The major relief because of calculators is that we don't have to do compound interest manually because that can take a long time. In the following article, you can learn about the interest for compounds and how you can calculate the interest for compounds within seconds with the use of our calculator.

Calculate compound interest formula in excel

STEP 1

1. Assume you set $100 into a bank. what proportion will your investment be worth without 1 year at an yearly rate of interest of 8%? the solution is $108.

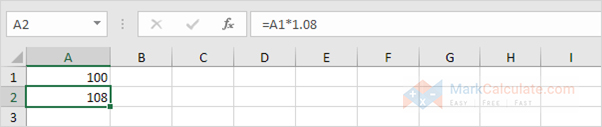
STEP 2

2. Now this interest ($8) moreover will earn interest (compound interest) next year. What proportion will your investment be worth without 2 years at an yearly rate of interest of 8%? The solution is $116.64.

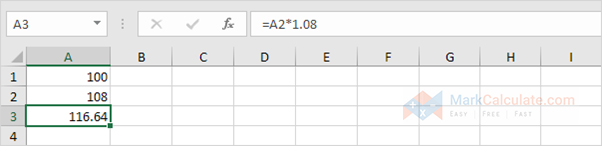
STEP 3

3. What proportion will your investment be worth without 5 years? Simply stilt the formula.
The wordplay is $146.93.

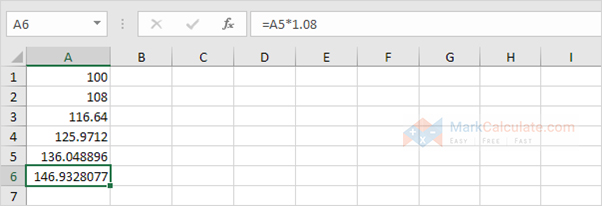
STEP 4

4. All we did was multiplying 100 by 1.08, 5 times. So we will moreover directly summate the worth of the investment without 5 years.

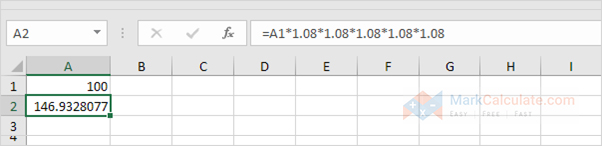
Which is that the same as:

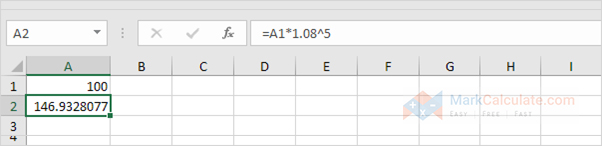
Note: there's no special function for interest in Excel. However, you'll hands create a interest calculator to match variegated rates and variegated durations.

STEP 5

5. Assume you set $100 into a bank. What proportion will your investment be worth without 5 years at an yearly rate of interest of 8%? You once know the solution.

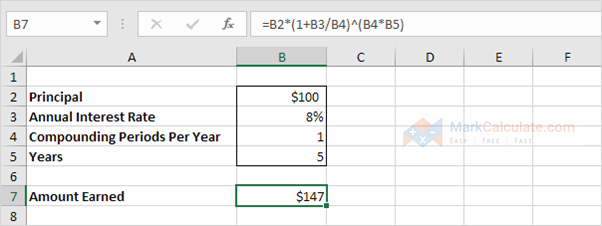
Note: the interest formula reduces to =100*(1 0.08/1)^(1*5), =100*(1.08)^5

STEP 6

6. Assume you set $10,000 into a bank. What proportion will your investment be worth without 15 years at an yearly rate of interest of 4% compounded quarterly? The solution is $18,167.

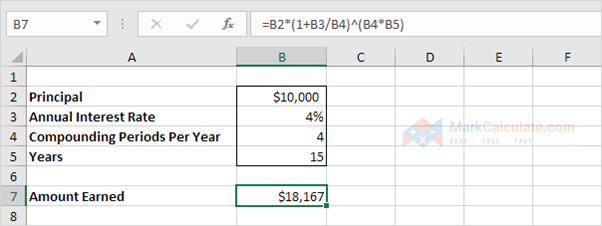
Note: the interest formula reduces to =10000*(1 0.04/4)^(4*15),
=10000*(1.01)^60

STEP 7

7. Assume you set $10,000 into a bank. what proportion will your investment be worth without 10 years at an yearly rate of interest of fifty compounded monthly? the solution is $16,470.

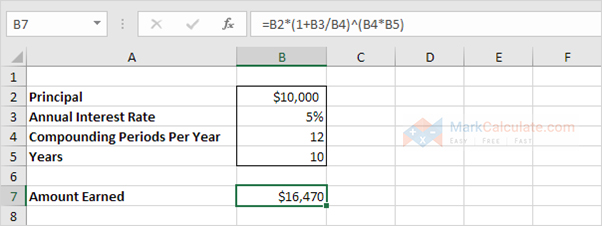
Note: the interest formula unchangingly works. If you're interested, download the Excel file and trammels out it yourself!

The factor which makes compound interest effective

Frequency of compound interest: The compounding frequency is significant. Highly regular cycles of compounding — for example, every day have dramatic effects. Search the accounts that accumulate every day when starting a deposit account. You will see only interest rates added annually to your record, but you will still make estimates every day. Any accounts only monthly or yearly quantify interest.

Time for annual compound interest: For long stretches, compound interest is more severe. Thus, as capital is used to expand independently, you have a larger number of computations or "credits to grow.

Interest rate yearly: An significant element in your equilibrium throughout time is perhaps the rate of interest. Higher Rate indicates that an asset is going to expand more rapidly. However, higher interest rates can be resolved through compound interest. Particularly for longer times, a compounding account with a lower rate will be ended up with the highest amount than a basic estimate.

Account deposits: Remittances and withdrawals will also impact your balance sheet and your account balance. This performs great to encourage your funds to increase or to introduce additional deposits to your list. You lessen the impact of compounding if you remove the income.

Rule of 72 (seventy two)

The guideline of 72 is some other way to make estimates approximately compound interest speedy. This rule of thumb tells you what it takes to double your money, looking on the fee you earn and the length of time you’ll earn that fee. Multiply the variety of years by using the interest rate. in case you get 72, you’ve were given a combination of factors that will about double your cash.

For instance 1: you have $1,000 in savings incomes five% APY. How lengthy will it take until you've got $2,000 on your account?

To locate the answer, determine out how to get to seventy two. When you consider that 72 divided by means of 5 is 14.4, it's going to take approximately 14.4 years to double your money.

For Instance 2:

You have $1,000 now, and you’ll want $2,000 in two decades. What price must you earn to double your money?

again, determine out what it takes to get to seventy two the usage of the statistics you have (the range of years). on the grounds that seventy two divided via 20 equals three.6, you’ll want to earn about three.6% APY to attain your aim.

Compound Interest Formula for Different Time Intervals

For a principal amount, compound interest can be computed for varying time periods using formulas applicable. In compound interest, the interest earned will differ depending on the period of computation.

Half Yearly

For half-year time period, interest is calculated in every 6 months, and the amount is compounded twice in a year.

Formula to calculate the compound interest for half-yearly time period, is as follows:

Q: Formula for compounded half yearly

Solution
Amount= Principal*{1+(r/2)/100)^n
r=rate of interest
n= conversion periods

Quarterly

For quarterly time period, interest is calculated in every 3 months, and the amount is compounded 4 times in a year.

Formula to calculate the compound interest for quarterly time period, is as follows:

P[1 + (r/4)^4t] – P

Monthly Compound Interest Formula

The monthly compound interest formula is actually the interest calculated per month. The monthly compound interest formula is given as:

CI = P (1 + r/12)12t - P

Overview of Compound interest formula

The compound interest formula calculator is a very relevant idea that allows you to realize where and how you handle your money and can also allow you to get a greater return on investment and savings. When interest is attached to the total gain of an asset, it, therefore, represents a compound interest, such that the general interest is attached to the capital number.

You can figure out just how often the compound interest will indeed be gained on your savings using this compound interest calculator, you can also use SIP calculator to find your returns on investments. You can measure the compound interest monthly, half-yearly, quarterly with this compound interest calculator , or though you prefer to calculate compound interest on one particular day. It plays a major role for an interest compound calculator that is interpreted and used by you as helpful and helpful by way of a compound interest calculator.

In today’s generation, we use a calculator for any sort of calculation because we had made ourselves very oriented on the outcome which should be more than 100 percent accurate, but manually it may not be as feasible or accurate as of the calculator. In making big predictions in seconds, calculators play a major role.

For example: Assume you make a 4-year investment of $40000 in a fixed deposit and a 10% (percent) interest rate so you will get about $4000 during the first year.

The major relief because of calculators is that we don't have to do compound interest manually because that can take a long time. In the following article, you can learn about the interest for compounds and how you can calculate the interest for compounds within seconds with the use of our calculator.

Conclusion

While using the online compound interest calculator of our website www.markcalculate.com you can obtain outcomes when using the compound calculator and guarantee that the knowledge you intend to enter is preparing so that you can achieve a real result using our calculator.